A step-by-step guide to understanding how to apply the concept of relative sizing to estimation, and then using that understanding to build backlogs at various levels of detail – from high level product road maps, through release planning, and onward with increasing levels of precision all the way down to detailed iteration planning…
Traditional Estimation
In traditional estimation models, a great deal of effort is expended at the beginning of the project to determine how long it will take to deliver everything in the project plan. These estimates are generally expressed in hours, and thus can be multiplied by a blended hourly rate to provide a cost estimate for the project.
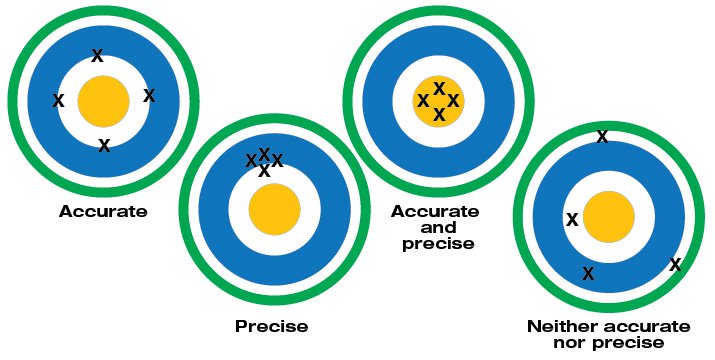
There is a general feeling among project managers, that due to the rigor that went into the estimation process these are ‘good’ or ‘accurate’ estimates. It is not uncommon to see a high level of ‘precision’ in the estimate. Even at a very high level of estimation, there is an attempt to create a relatively small ring of uncertainty around the estimate (see Figure 1). Ironically, any illusion of precision is erased almost immediately as those estimates are padded with contingent time to account for any problems with the accuracy. Another trick is to utilize future change requests as opportunities to ‘correct’ the highly precise, yet potentially inaccurate estimates. The longer the project, the more opportunities there are to adjust.
Unfortunately, it’s just as likely that on a longer project, there will be some work that is designed and estimated that will not be completed due to changing project needs. There is little recourse to protect against this outcome.
There are some recognized shortcomings in traditional estimation. Most prominent among them is the fact that traditional estimates are not portable – an estimate in hours made on behalf of one person, is very likely to change if it is performed by another person. Considering the amount of time we spend creating traditional estimates and the longer timeframe of these efforts, there is a fair amount of risk that the team makeup will change before the feature is built, further reducing the effective accuracy of these estimates. In other words, we spent a lot of time making a very precise estimate that is wrong. This is wasteful.
Agile Estimation
Agile development methods and models all evolved from a common origin in Lean manufacturing techniques.
One of the driving tenets of Lean is the relentless removal of waste from a system. If traditional estimation models lead to waste, then Lean demands we find a way to reduce, if not outright eliminate that inefficiency.
One way to avoid waste in estimation is to reduce the amount of time spent making the estimate. As noted earlier, there are two factors when it comes to judging an estimate: Accuracy and Precision. Our first duty is to get the estimate into the right ballpark – to have it be accurate-ish. Our second duty is to reduce the uncertainty – to make it more precise. There is a cost to higher levels of precision. The longer you spend working on an estimate, the more you can learn about what is needed and the higher the degree of precision – however, you will eventually reach a point of diminishing return. Yes, spending time on the estimate will tighten the circle, but the degree of improvement will be less and less with each unit of time spent learning. In effect, the cost of gaining precision will begin to exceed the cost of the variance in the estimate. Figure 2 illustrates this point, a 5% improvement in the estimate takes only 10 minutes in the beginning, but the next 5% takes an hour, the next 5% takes a day.
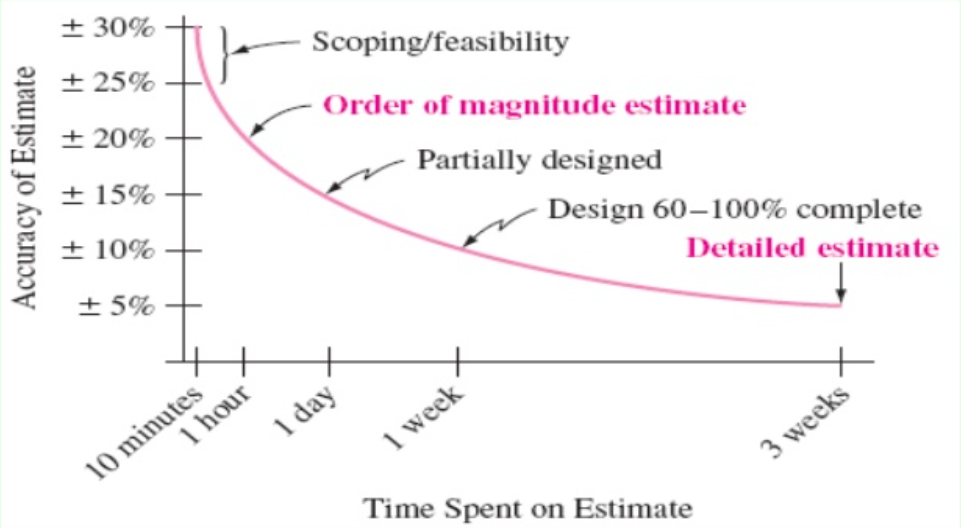
If we gather an estimate for something that we will never implement, the time spent gathering that estimate is by definition wasted. We should try to reduce waste as much as possible. The farther out on the planning horizon a deliverable is, the more likely something else will get in the way before we get to it. As time passes it becomes less likely that something else will get in the way, and therefore more likely that the item will be implemented. It stands to reason that estimates on things far out on the planning horizon should be as fast as possible, then as we get closer to actually implementing that item, we spend a little more time to get a more precise value. We can repeat this procedure as it grows nearer, incrementally spending a little more time with the feature, adding detail to our understanding, and precision to our estimate.
There are multiple levels of estimation, and each level provides an increasingly level of precision in the estimate. In the model being proposed, the three levels are shown in Figure 1.3.
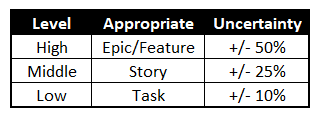
For the first two levels of estimation (High Level and Middle), we use a concept called ‘relative’ sizing. Relative sizing is a practice that allows changes in understanding to be reflected in estimates without re-estimation being required. ‘How is that possible’, you may ask?
Relative Sizing
In general, people are not very good judging the exact size of a thing just by observation, but they are very good at judging between the relative sizes of two things. You’ve been doing this since you were young – especially if you have siblings. Children spend a lot of time evaluating their place in the world relative to others. If there was a choice between two pieces of chocolate cake, you immediately knew which was the bigger one or if the difference in size was so small, as to be insignificant. Relative sizing of features leverages that same innate skill. You may not be able to tell me the exact size of a thing just by looking at it, but you sure can look at two things and identify whether one is bigger, smaller, or about the same as the other.
That same skill can be leveraged to gauge the relative magnitude of two things. If I give you a choice of two objects where one is clearly larger than the other, you won’t need a measuring tape to tell me that one of them bigger than the other. You could probably even tell me if one was more than twice as big as the other!
To illustrate why we use this relative sizing instead of absolute, consider this example:

Let’s say we’re estimating the size of an object…something innocuous, like a tennis ball, and let’s further imagine that we have three people being asked for estimates. Let’s go a step further, and say that I do all my measuring in inches, you do all your measurements in feet, and my offshore team does all their measuring in centimeters. Crazy, right? The result of this, is that without consulting with each other, it’s likely that we’ll come up with three radically different numbers. I might say it’s a “2.7”, you call it “1/6th”, and the offshore team calls it a “7”. There are probably some folks out there who would find this mixture of measurement units undesirable. But the truth is, as long as we’re each working in our own world and have no need of passing work from one team to another, we’d be fine. I literally don’t need to care what your unit of measure is, unless we ever have to have a discussion with each other about it. What do you suppose would happen if I ask the offshore team to take on this Size 2.7 item? There is a real risk they could just say ‘yes’ without realizing my scale is different, and suddenly get surprised to learn that this thing is more than double the effort of the 3 they thought they were getting.
To get around that problem, we need a different unit of measure, and in a shared workspace, we want that to be a common unit of measure as well (i.e., everyone agrees to use it). It’s a common point of contention about whether metric or imperial units of measure are more appropriate. The argument is long and tedious. It could go on for miles … er kilometers … I mean… why do this to ourselves? What if we didn’t have to choose?

When we compare a golf ball to a tennis ball, we could easily say the tennis ball is bigger than the golf ball, and if pressed, we could take it a step further and say it is twice as big as the golf ball. If I have a container that holds a dozen golf balls, then based on our thumbnail comparison, I could probably surmise the container will hold half as many tennis balls as golf balls… or six tennis balls.
Now here’s the interesting part. If YOU have a container that holds ten tennis balls, do we need to re-estimate the ball sizes or can we infer that your container will hold close to twenty golf balls? Further, if my offshore team has a duffel bag that holds 50 tennis balls, I don’t need to convert the interior dimensions of their bag from cubic cm to cubic feet or inches to be able to estimate how many golf balls will fit in there. We already have established that tennis balls take up twice as much space as golf balls. As long as we have an agreed upon frame of reference, this is pretty simple. And it’s simple because the balls didn’t change size. It is the capability of each container to carry the balls that is different!
Let’s take a moment to define a couple of terms. We’ll refer to the ‘size’ we estimated our balls in as a “Ball Point”. The ball point has nothing to do with the exact dimension of the balls. It is a new unit of measure. A golf ball is one ball point, and a tennis ball is 2 ball points, because it is twice as big as a golf ball. The number of ball points we believe will fit in our container is the container’s “Capacity”. Because a tennis ball is 2 ball points, and my container holds 6 tennis balls, the capacity of my container is 12. Keep in mind that you will always encounter people who believe your container can hold more balls, and they’ll encourage you to put more and more into your container. This can result in an unstable situation where balls may fall out of the container. The number of ball points that actually get delivered without being dropped or damaged is the “Velocity”. Note the distinction: Capacity is theoretical forward-looking (Plan-based), Velocity is based on practical observation of results (Outcome-based).
Relative sizing helps get us past a lot of hand-wringing about specific differences between two items. What if you and I are talking, and I make the bold statement that I think a golf ball is 1 inch in diameter. By my rough, relative sizing, that would mean a tennis ball (observably twice its size) must be around 2 inches in diameter. You could counter that you think a tennis ball is closer to 3 inches in diameter; therefore a golf ball is closer to 1.5 inches. Do we gain anything from this discussion? We’re still basing our estimates on observation alone. Unless something changes, more discussion isn’t going to improve our estimates. Even more importantly, the fact that we made those bold statements of dimension didn’t change the capacity of our respective containers, did it?
Let’s consider this: As certain as we are in our estimates, we’re both objectively wrong, or at least objectively inaccurate (the Golf ball is actually 1.68 inches, and the Tennis ball is 2.7 inches). But if you’ll excuse the pun, we’re in the ballpark! Remember, we are providing an estimate, not an actual. We don’t need to know the exact measurement of either ball to do estimation with relative sizes. We know from observation that my container holds six tennis balls, yours holds a dozen, and the offshore team holds closer to twenty-five. The (really important) point here, is that none of us needs to know the exact measurement of the tennis ball!
If we assume a margin of error to our estimate, then things get even better. Instead of saying that we’re estimating an exact size, we are estimating a value that falls in a range… maybe +/- 25%

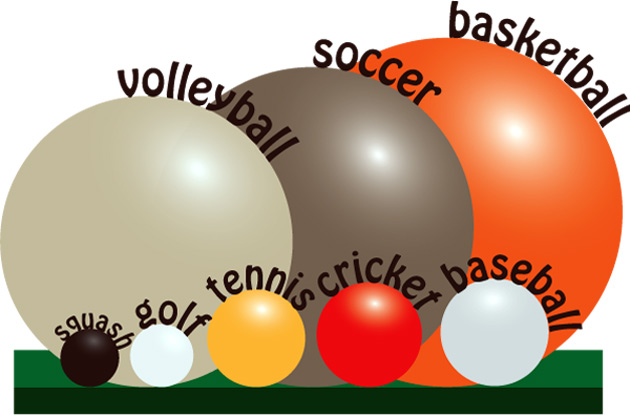
The first two balls give us a decent starting point, but it’s hardly the full universe of balls. Let’s put a bunch of balls out on the table, and group them by those that are close to each other in size. If we did that, we’d probably group the Squash, Ping-Pong and Golf balls together. We’d group the Tennis, Cricket, and Baseballs together. Croquet, Softball and Bocce are together. The volley, bowling and soccer balls are close enough to each other to form a group. The Basketball is largest overall, but both the football and rugby ball are longer. One could argue the football is more complicated, so we can use its oddness to justify going with the longer dimension as our estimate. Now for the magic: We can very quickly, decide that the smallest group of balls will be “1’s”, the second grouping is roughly twice that size, so they’re “2’s”. The next group are “3’s”, and the next group are “5’s”. The last group is “8’s”. By strict observation, these are reasonable groupings. There’s also an odd, in-between size. Both Racquetballs (and Billiard balls) are firmly between the Golf and Tennis groups. For something on the line, we’ll err on the side of caution and promote these items to the higher group, in this case making them “2’s”.
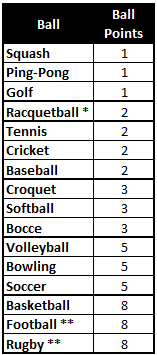
Calibration
Let’s think back to our example with everyone using different units of measurement. Nobody was really wrong; they just spoke different languages when it came to estimates. What if we took all three of the individuals aside, threw a golf ball on the table, pointed to it and said, “One. That Golf ball is a One. We’re all agreeing to call it a One. If the Golf ball is a One, what’s the Ping-Pong ball?”
We would expect everyone to say “One”.
Then you toss a Tennis ball on the table. “What’s that?”
“Two”
“Good. From now on, we need you guys to shift your way of thinking to this scale, so we can more easily communicate and share work with each other.”
To put that another way, the shift must be made from thinking about relative size as related to the physical measurement of a thing, and instead by looking at the relative magnitude of it. It doesn’t matter how many inches, millimeters or hectares big a thing is if we can say it is 1, 2, 3, 5, or 8 times the size of a reference we all agree on.
Validation
Some of you reading this, have intuitively recognized the value of relative sizing and therefore don’t require further proof. If you count yourself among the enlightened, feel free to skip this section. On the other hand, for the doubters among you…
I don’t normally advocate this next step, but it seems a lot of people prefer to validate their assumptions before accepting a new method. So if we must break from the spirit of relative sizing by whipping out a measuring stick, I’d much rather you did it with the balls, than with actual user-stories.
Let’s try checking our work and actually measure some of the balls. If we take all the balls in each group, and average them, then throw a 25% window around that average, you’ll create ranges that you can use confirm the limits of each range. The earlier hand-wringing we observed over whether a racquetball belongs as a 1 or 2 is seen here as well. It clearly falls on the cusp between the two ranges. In times like this it is faster to just err on the side of caution and round it up to the next larger size.
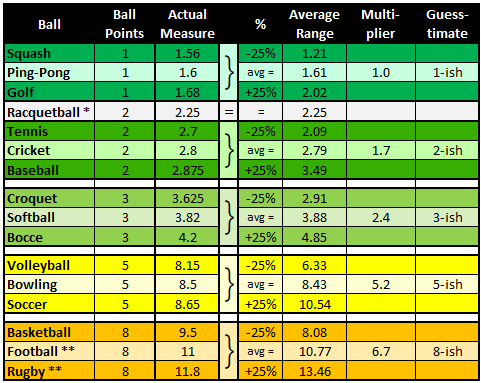
Note: This is an unnecessary level of calculation. There is no absolute relationship between ball points and size. There is only an approximate relationship. Don’t look for anything deeper than that.
This was an interesting intellectual exercise, but its real value is in the fact that we verified that our relative groupings were “close enough”, and we don’t ever need to do this again. (Trust me; it’s an agile anti-pattern for a reason!) When we’re estimating a lot of things, the ability to do so quickly becomes important. Hopefully, this exercise will reassure you that you don’t need to worry too much about the exactness of your estimates. A range of uncertainty is an acceptable trade-off for the increase in speed!
Are You With Me So Far?
On the one hand, you could accuse me of avoiding a fight between the inch and centimeter folk, by introducing a unit of measure that neither wanted. I would allow that, but I want to remind you about the question that started this discussion off. Remember, we were talking about how much effort goes into estimation, and how we want to shorten the time spent making estimates — seeking that sweet spot between effort and precision. I suggest to you that by avoiding the argument over units, I’ve made it possible for people to toss their favorite ruler out the window, and start thinking about size as an abstract concept.
Hopefully, this introduction to relative sizing makes sense and demonstrates how we can use relative sizing to produce a faster estimate, and through calibration we can produce portable estimates. It’s pretty cool, isn’t it?
But this is only the beginning of our agile estimation journey. In the next section I’ll demonstrate how to use relative sizing to create meaningful roadmaps and release plans.


